​高等数学不定积分，你学会了吗？第一类换元积分，都讲了些什么？

高等数学不定积分，你学会了吗？第一类换元积分，都讲了些什么？

想必大家对于大学数学中，不定积分的概念，应该不是很陌生吧？

我们首先来看一下，不定积分的概念：

定义：函数f(x)的所有原函数称为f(x)的不定积分，记作∫f(x)dx，如果F(x)是f(x)的一个原函数，那么就有∫f(x)dx＝F(x)＋C成立。

我们将讲述式子进行拆分，可知每一部分的表述如下。

∫→积分号；f(x)→被积函数；

X→积分变量；f(x)dx→被积表达式；

C→积分常数；

了解完了不定积分的概念，我们来看一下第一类换元积分法到底要怎么运用。

按照一般情况：假设F'(u)＝f(u)，则∫f(u)du＝F(u)＋C，且u＝φ(x)(可微)。

因为：dF[ φ(x)]＝f[φ(x)]φ'(x)dx

所以可得关系式：∫f[φ(x)]φ'(x)dx＝F[φ(x)]＋C＝[ ∫f(u)du ]u＝φ(x)

根据上面的过程，可得换元法定理。

这就是我们今天要学习的内容，将复合函数求不定积分用换元法进行求解，这个求解过程称为第一类换元积分法。

接下来，我们来看一下换元定理。

定理：设f(u)具有原函数，u＝φ(x)可导，则有换元公式如下：

∫f[φ(x)]φ'(x)dx＝[∫f(u)du]u＝φ(x)

上述公式就是我们这节课要用到的第一类换元公式《微分法》

注意：在使用这个公式时，关键在于将不定积分进行转化,例如：∫g(x)dx化为∫f[φ(x)]φ'(x)dx

在用第一类换元公式（微分法）转化时，观察的重点不同，那么得到的结论也是不同的。

接下来，我们来看一下例题，以加深理解。

例题一、∫sin2xdx

分析：对于该例题一共有三种解法，第一种解法，我们在求解时，可以采用以上的换元法进行转化，可以另u＝2x，那么就可以将式子进行转换，则sin2x＝sin u，然后再根据配凑法进行配平即可。凑1/2d(2x)＝dx

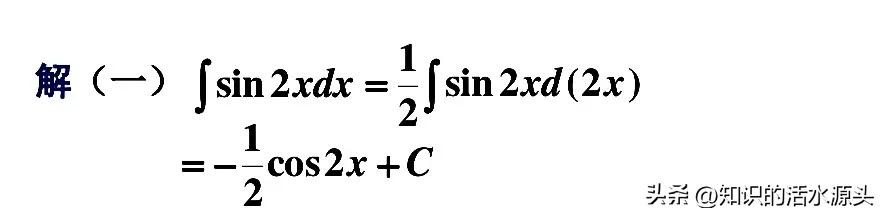
第二种解法，求解之前，我们将式子进行转换，变成sin2x＝2sinx cosx，然后再进行求解，进行凑微分即可求的答案。凑(cosx)dx＝d(sinx)

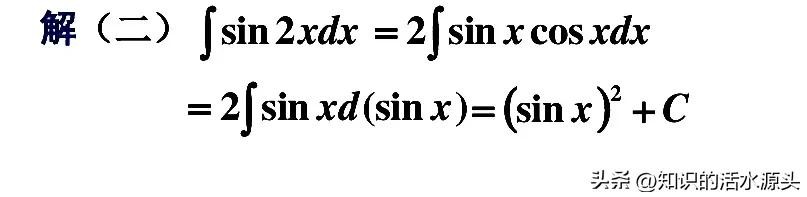
第三种解法，同第二种解法一样，先转换sin2x＝2sinx cosx，然后再进行求解，进行凑微分即可求得答案。凑(sinx)dx＝－d(cosx)

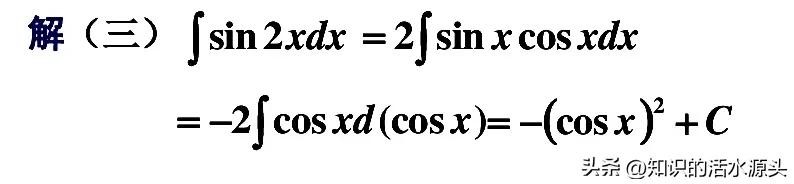
例题二、∫1/(3＋2x)dx

分析：这个题目是分子为1，分母为(3＋2x)的分数，要想解决这个题目的不定积分，可以将其凑为(lnu)'＝1/u的形式。

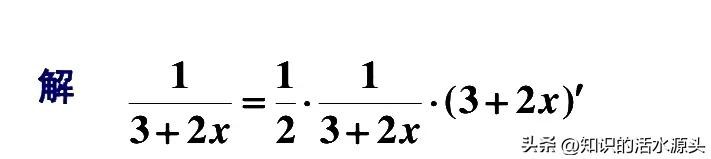
所以可以先进行凑微分，然后再进行配平，根据凑微分，1/2×d(3＋2x)＝2×1/2dx

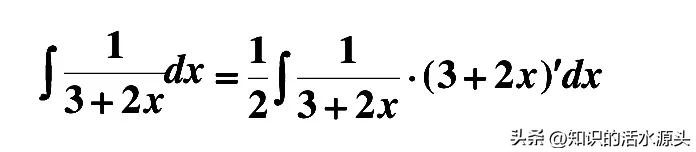
此时就可以得到对数函数求导的基本模型。

一般情况，只要是符合以下情况，都是可以进行找常数的倒数，然后进行配平。

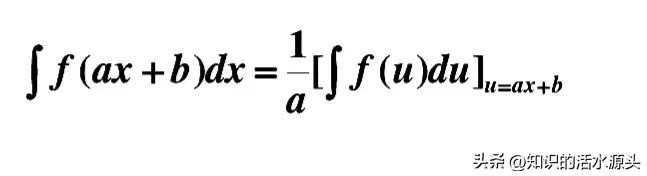
例题三、∫sin²x cos⁵x dx

分析：这是正弦函数和余弦函数相乘，并且是次方形式，当遇到这种情况，被积函数是三角函数相乘时，需要拆分奇次项，然后进行凑微分。此时可得cos⁵xdx＝cos⁴ x cosxdx＝cos⁴xd(sinx)

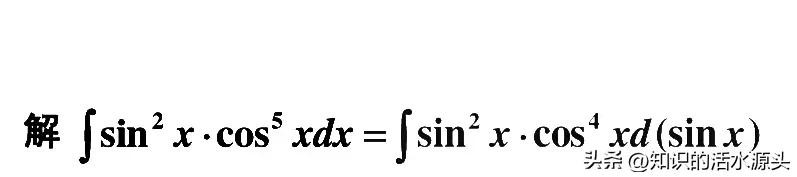
凑微分后，大家会发现，既有正弦函数也有余弦函数，此时还是不能直接展开，最好的方法就是将余弦函数变换成正弦函数形式，这要用到三角代换cos² x＝1－sin²x，然后用完全平方差公式展开即可(a－b)²＝a²－2ab＋b²

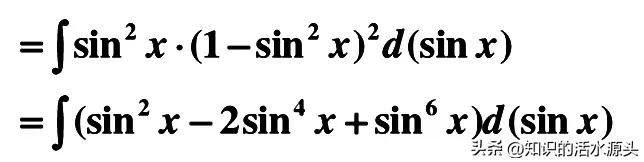
展开后，大家会发现，这个不定积分可以根据积分的加减法运算法则变换成三部分，这三部分的积分运算，实际上就是幂函数求不定积分的运算过程。

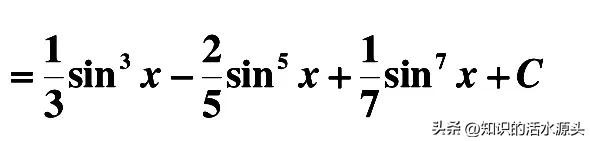
例题四、∫cscxdx

这个题主要是对余割函数求不定积分，在这里大家可以采用代换的方法进行求解，将余割函数代换成正弦函数，cscx sinx＝1⇌cscx＝1/sinx，然后再进行凑微分即可。

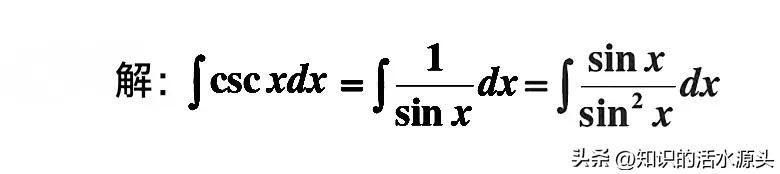
这里凑微分要注意的是，先在分子和分母进行乘正弦函数sinx，凑sinxdx＝－d(cosx),然后将被积函数变换sin²x＝1－cos²x 。

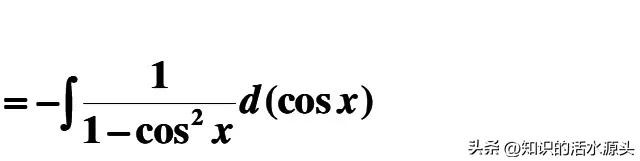
到这一步就很简单了，我们另u＝cosx，将式子裂项1/(1－u²)＝1/2×[1/(1－u)＋1/(1＋u)]，裂项后再进行配平即可。

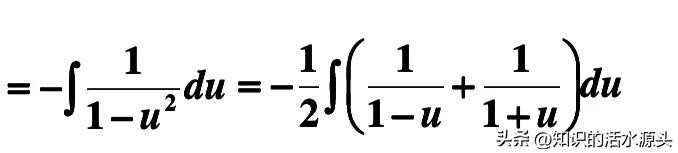
根据上述式子，我们可以将其展开，然后成为两项，这时候再进行凑微分，然后根据对数函数求积的形式进行解答即可。这里要注意一个很重要的关系式ln(1－u)－ln(1＋u)＝ln(1－u/1＋u)。

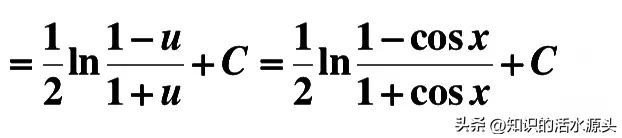
夯实基础，练习达标：根据提示，大家试一试以下题目应该怎么做。

大家下去过后，可以尝试解答一下这些练习题，有不明白的留言讨论。