数学中无穷级数的奥秘

01 几何级数

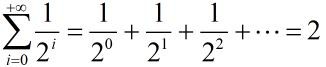
Σ是求和公式，也是欧拉大神所创，上面给出的式子叫几何级数，什么叫级数呢？

简单说，级数就是把数列各项用加号连接起来的函数，比如几何级数就是：

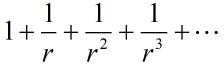
这货跟几何有什么关系呢？为什么叫几何级数，以r=2为例吧，话不多说直接上图：

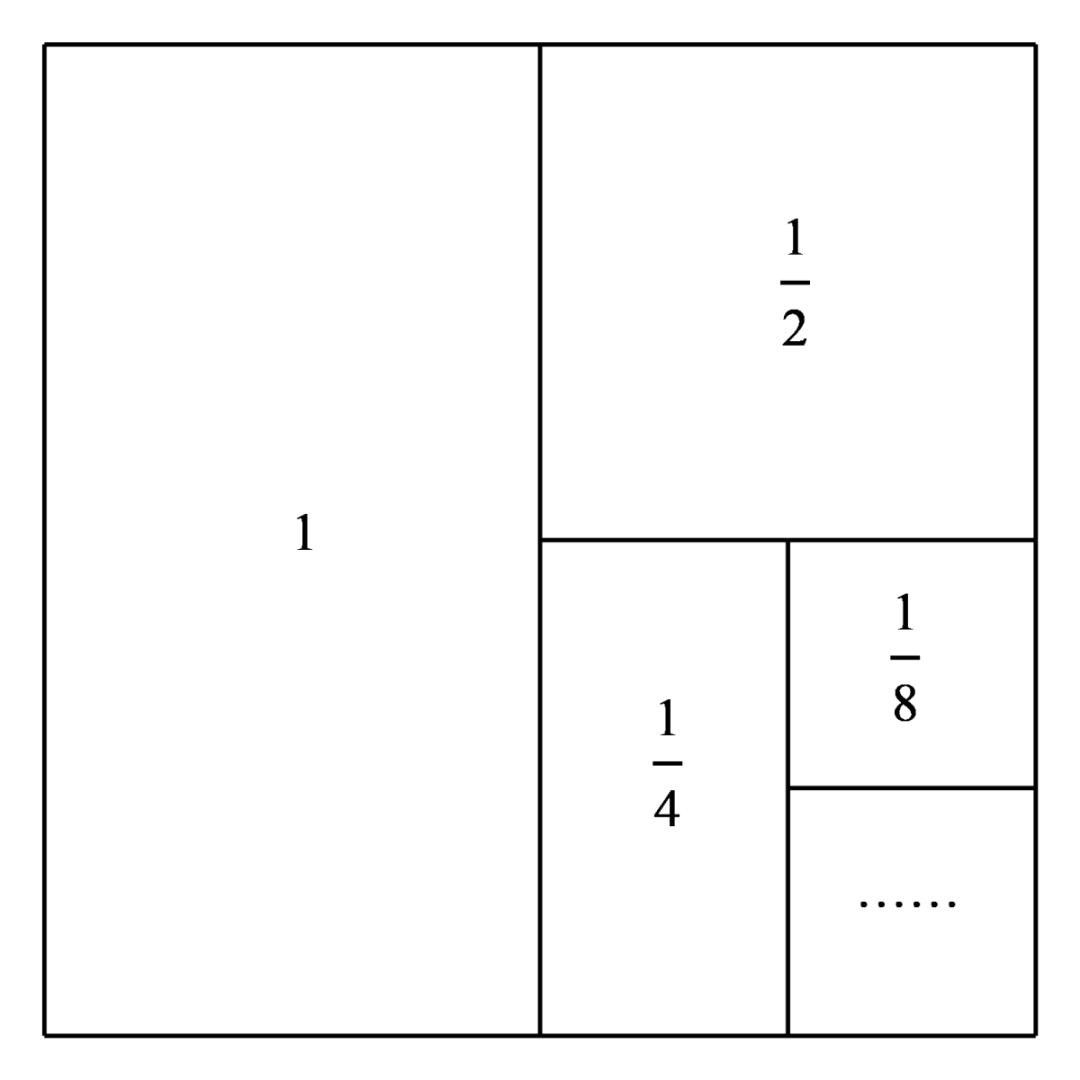
这是一个面积为2的正方形，可以分割成如图的一些小矩形的面积之和，按这样切割的顺序一直加下去，便有了：

当然可能会有同学质疑说这么一直加下去怎么就等于2了呢？为什么不是小于2？

利用等比数列求和公式：

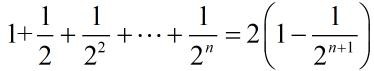
当n无穷大时，我们认为：

不用纠结这个，因为这便是最好的结果。

当然如果实在说服不了自己的话，就换个思路想，这个算式的结果不可能大于2吧，也无法说明其小于2，如果小于，小多少呢？所以只能承认

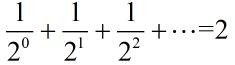
这是阿基米德说的。

类似这样的思路，考虑设计：

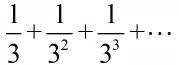
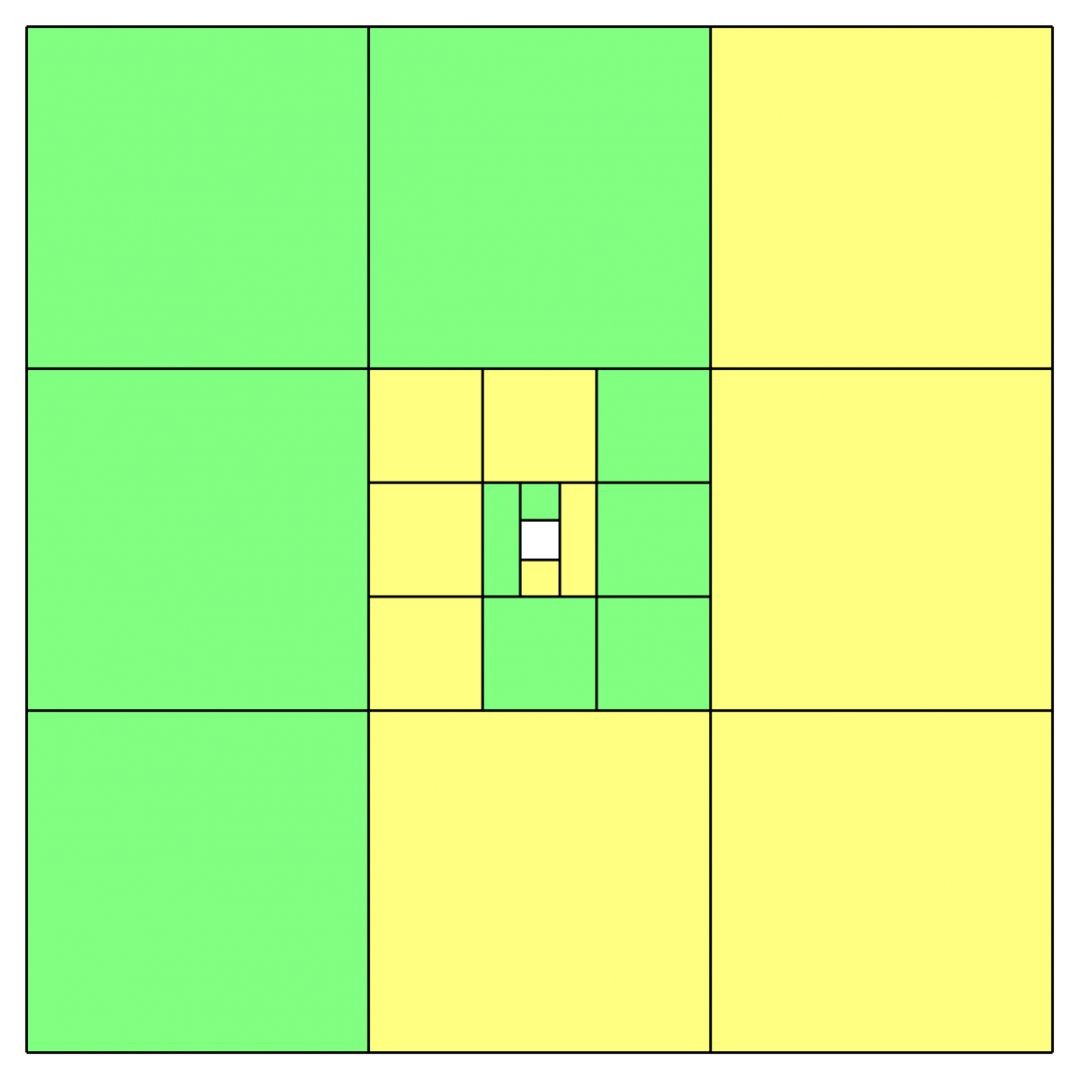
在这里，大正方形的面积为1，绿色部分和黄色部分是对对称的两部分，足以说明：

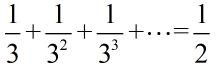
再来个

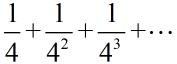
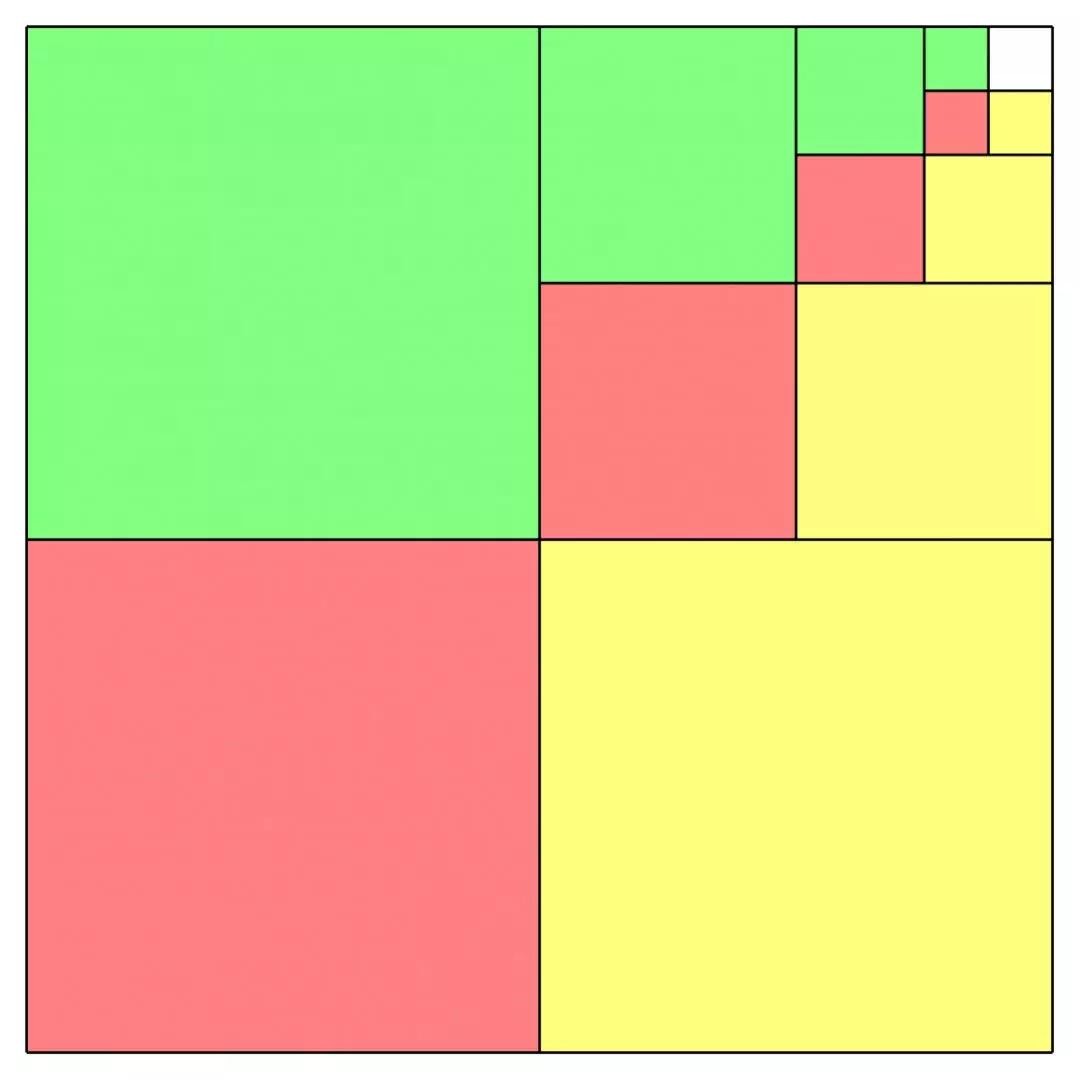
大正方形的面积为1，所以最后的结果是1/3！

02 无穷相加的必要条件

几何级数因为是无限相加，所以也叫无穷级数，如果“级数”这个词看着别扭，就理解为是无穷个数相加好了。既然是加法当然我们要求结果啦，求不出结果的式子其存在毫无意义，所以会有求不出结果的式子吗？

还真的有！

S=1-1+1-1+1-1+……

S的值为多少？

法1：S=（1-1）+（1-1）+（1-1）+……=0

法2：S=1+（-1+1）+（-1+1）+……=1

法3：S=1-（1-1+1-1+1-1+……）=S，∴S=0.5

哇塞，竟然想出了三种方法！

哇塞，三种方法的结果居然还不一样！

那哪个是正确答案？感觉这三个看起来都有道理，作为一门严谨的学科，最怕感觉这么回事，因为感觉是不讲道理的，偏偏数学要以理服人。

其实这三种做法都用到了“加法结合律”！什么是加法结合律，这应该是小学内容了吧：a+b+c=a+（b+c）

在计算加法的时候可以先把后面的部分先加起来，但要注意的是，我们所说的计算都是有限个数的计算，而我们上面的题目可是求一个无穷级数的结果，所以问题就出在这里！

我们不能拿有限数的计算方法用在无限当中，这便是我们没有感觉出有差别的地方。讲真，察觉不出这一点很正常，但不要习以为常，对于计算的每一步，请考虑是否完全等价！

所以以上都不是正确答案，这个算式没有答案。在无穷的世界里会有很多我们想象不到的结果，比如整体可以等于部分，比如说无穷也分可数与不可数等等，所以出现这样没有结果的结果也不用太意外了。

那什么样的无穷相加才会有结果呢？我们想要的结果当然是一个数咯，稍微分析一下我们就会发现，这串数列后面的数必须得越来越小，在无穷处趋近于零，即我们所谓的极限为0，这样才能有个结果。

正如前面所举的例子：

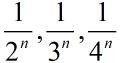
这些当n趋近于无穷大时，结果都为0，这样才有可能得到一个数字作为结果，像这样的级数称为是收敛的。

反观1+1+1+1+……，结果便只能是无穷大，并不能得到一个确定的数字。像这样的级数我们称为是发散的。

那是不是只要满足这一串相加的数列的极限为0就好了呢？

03 必要不充分

计算：

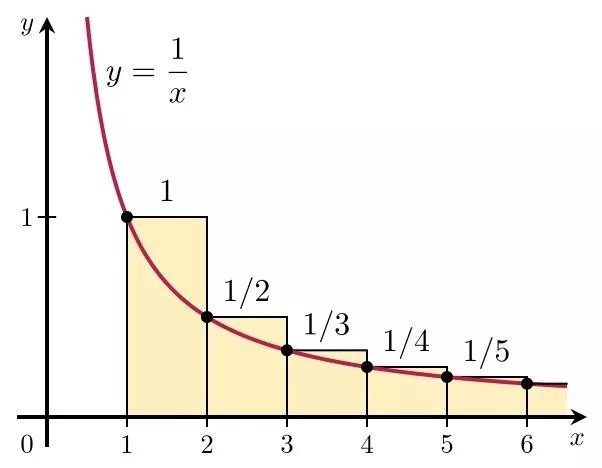
这个级数我们称为叫调和级数，一直加下去，结果会是多少呢？

感觉一下？

结果等于正无穷，因为

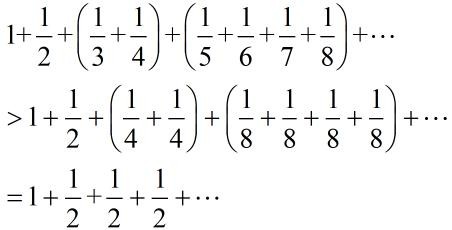
所以想要结果有多大就有多大，也就是说即便这串数列的极限为0也不能保证一定由结果。

再比如还可以这么解释：

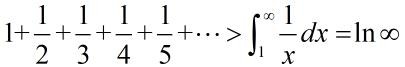
所以调和级数是发散的。

因而数列极限为0仅仅是必要条件（想要有结果必须得满足这个），还不够充分（即便满足这个也不一定有结果），并不能保证一定有个结果。

不过既然是必要条件，说明还是会有一些例子是可以求得结果的。

著名的“贝塞尔”问题

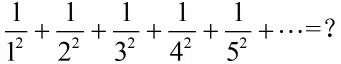
首先这个结果肯定不会无穷大，用我们初中知识便可以解决：

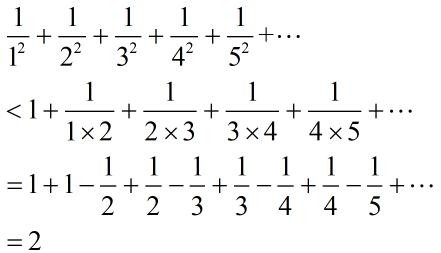
欧拉大神说：

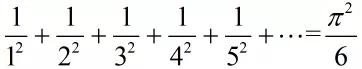
什么？这玩意怎么和π还有关系！

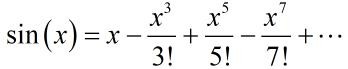
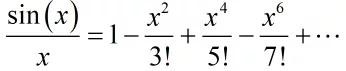
因为sinx/x的解集为

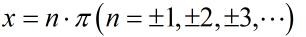
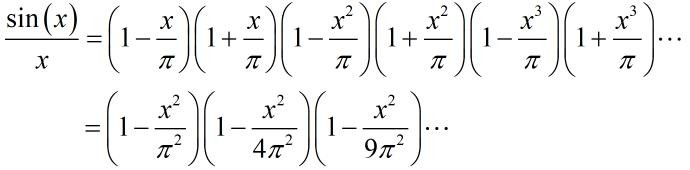
考虑x²项系数对应相等，即有：

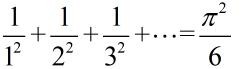
虽然证明过程还略有不完善之处，但瑕不掩瑜。

04 补上答案

作为一个问题的完整回答，必须得再补上问题的正解，对于级数

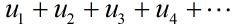
记：

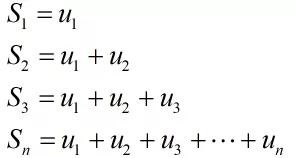
这里的Sn称为前n项和，既然是求和，不妨一步一步来，我们想要的结果是一个确定的数值，那就从前n项和的规律来探讨。

当n趋近于无穷大时，若Sn的极限存在，则此极限便是无穷级数的结果。

所以所谓的无穷相加的结果，即是前n项和的极限，若极限不存在，则亦不存在相加的结果。

在无穷面前，我们的想象力确实有一点渺小。